Koden for denne bloggen, sammen med datasettet, er tilgjengelig på følgende lenke https: // github.com / shekharpandey89 / k-betyr
K-Means-klynging er en maskinlæringsalgoritme uten tilsyn. Hvis vi sammenligner K-Means uovervåket klyngealgoritme med den overvåkede algoritmen, er det ikke nødvendig å trene modellen med merkede data. K-Means algoritme brukes til å klassifisere eller gruppere forskjellige objekter basert på deres attributter eller funksjoner i et K antall grupper. Her er K et heltall. K-Means beregner avstanden (ved hjelp av avstandsformelen) og finner deretter minimumsavstanden mellom datapunktene og sentrumsgruppen for å klassifisere dataene.
La oss forstå K-midlene ved hjelp av det lille eksemplet ved hjelp av de 4 objektene, og hvert objekt har to attributter.
| Objektnavn | Attributt_X | Attributt_Y |
|---|---|---|
| M1 | 1 | 1 |
| M2 | 2 | 1 |
| M3 | 4 | 3 |
| M4 | 5 | 4 |
K-midler for å løse numerisk eksempel:
For å løse det ovennevnte numeriske problemet gjennom K-Means, må vi følge følgende trinn:
K-Means-algoritmen er veldig enkel. Først må vi velge hvilket som helst tilfeldig antall K og deretter velge sentroider eller sentrum av klyngene. For å velge sentroider kan vi velge hvilket som helst tilfeldig antall objekter for initialiseringen (avhenger av verdien av K).
De grunnleggende trinnene for K-Means-algoritmen er som følger:
- Fortsetter å løpe til ingen gjenstander beveger seg fra sentroidene (stabile).
- Vi velger først noen sentroider tilfeldig.
- Deretter bestemmer vi avstanden mellom hvert objekt og sentroider.
- Gruppere objektene basert på minimumsavstand.
Så hvert objekt har to punkter som X og Y, og de representerer på grafområdet som følger:
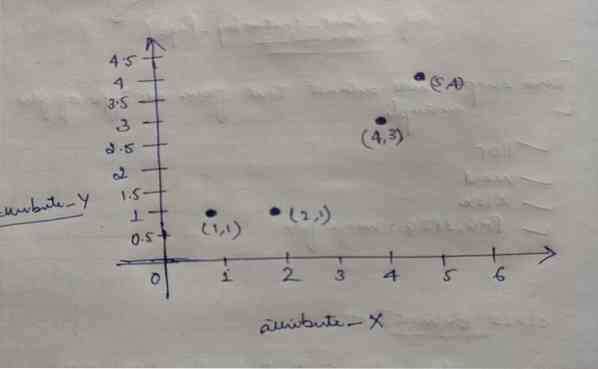
Så vi valgte i utgangspunktet verdien av K = 2 som tilfeldig for å løse problemet vårt ovenfor.
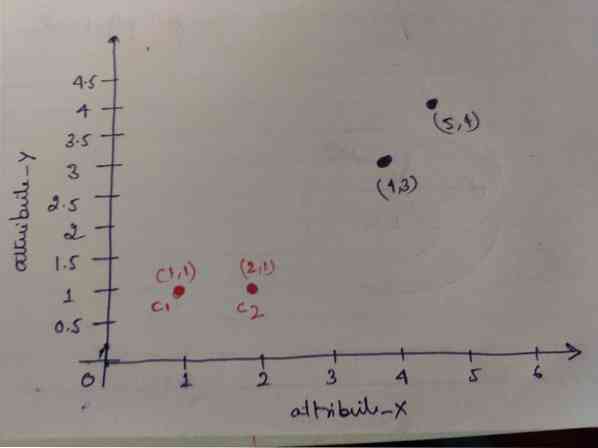
Trinn 1: I utgangspunktet velger vi de to første objektene (1, 1) og (2, 1) som våre sentroider. Grafen nedenfor viser det samme. Vi kaller disse sentroidene C1 (1, 1) og C2 (2,1). Her kan vi si at C1 er gruppe_1 og C2 er gruppe_2.
Trinn 2: Nå skal vi beregne hvert objektdatapunkt til sentroider ved hjelp av den euklidiske avstandsformelen.
For å beregne avstanden bruker vi følgende formel.

Vi beregner avstanden fra objekter til sentroider, som vist på bildet nedenfor.

Så vi beregnet hvert objektdatapunktavstand gjennom avstandsmetoden ovenfor, til slutt fikk vi avstandsmatrisen som gitt nedenfor:
DM_0 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) klynge1 | gruppe_1 |
| 1 | 0 | 2.83 | 4.24 | C2 = (2,1) klynge2 | gruppe_2 |
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Nå beregnet vi hvert objekts avstandsverdi for hver sentroid. For eksempel har objektpunktene (1,1) en avstandsverdi til c1 er 0 og c2 er 1.
Fra avstandsmatrisen ovenfor finner vi ut at objektet (1, 1) har en avstand til klynge1 (c1) er 0 og til klynge2 (c2) er 1. Så objektet en er nær selve cluster1.
Tilsvarende, hvis vi sjekker objektet (4, 3), er avstanden til klynge1 3.61 og til cluster2 er 2.83. Så objektet (4, 3) vil skifte til cluster2.
Tilsvarende, hvis du ser etter objektet (2, 1), er avstanden til klynge1 1 og til klynge2 er 0. Så dette objektet vil skifte til cluster2.
Nå, i henhold til avstandsverdien, grupperer vi poengene (objektklynging).
G_0 =
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | gruppe_1 |
| 0 | 1 | 1 | 1 | gruppe_2 |
I henhold til avstandsverdien grupperer vi poengene (objektklynging).
Og til slutt vil grafen se ut som nedenfor etter å ha gjort klyngingen (G_0).
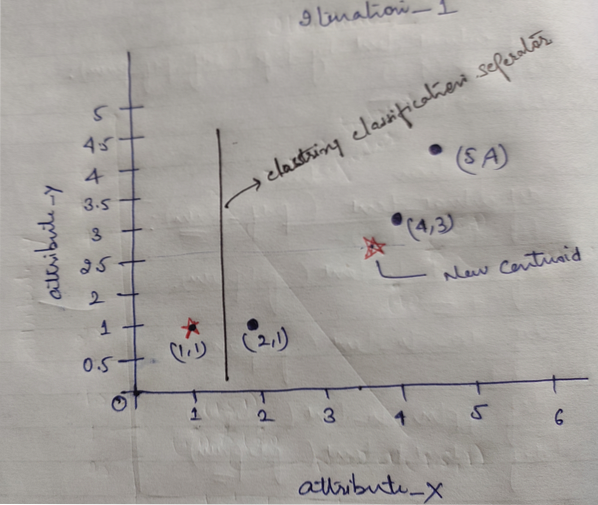
Iterasjon_1: Nå skal vi beregne nye sentroider etter hvert som gruppene ble endret på grunn av avstandsformelen som vist i G_0. Så, group_1 har bare ett objekt, så verdien er fortsatt c1 (1,1), men group_2 har 3 objekter, så den nye sentrumsverdien er 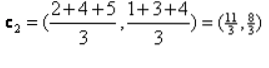
Så, nye c1 (1,1) og c2 (3.66, 2.66)
Nå må vi igjen beregne hele avstanden til nye sentroider som vi beregnet tidligere.
DM_1 =
| 0 | 1 | 3.61 | 5 | C1 = (1,1) klynge1 | gruppe_1 |
| 3.14 | 2.36 | 0.47 | 1.89 | C2 = (3.66,2.66) klynge2 | gruppe_2 |
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Iteration_1 (klynging av objekter): Nå, på vegne av beregningen av den nye avstandsmatrisen (DM_1), klynger vi den i henhold til det. Så vi skifter M2-objektet fra group_2 til group_1 som regel om minimumsavstand til sentroider, og resten av objektet vil være den samme. Så ny klynging blir som nedenfor.
G_1 =
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | gruppe_1 |
| 0 | 0 | 1 | 1 | gruppe_2 |
Nå må vi beregne de nye sentroidene igjen, da begge objektene har to verdier.
Så, nye sentroider vil være 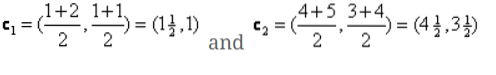
Så etter at vi har fått de nye sentroidene, vil klyngingen se ut som nedenfor:
c1 = (1.5, 1)
c2 = (4.5, 3.5)
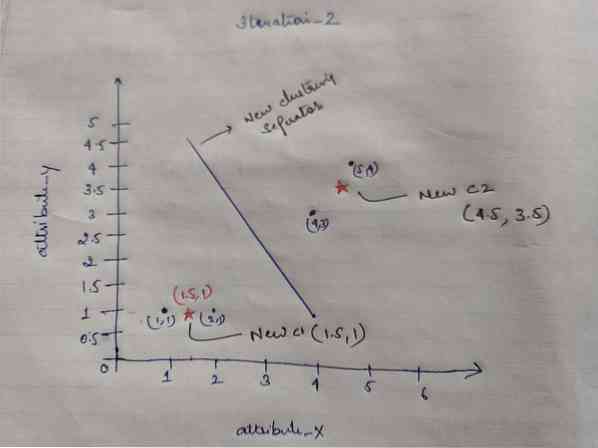
Iterasjon_2: Vi gjentar trinnet der vi beregner den nye avstanden til hvert objekt til nye beregnede sentroider. Så etter beregningen vil vi få følgende avstandsmatrise for iterasjon_2.
DM_2 =
| 0.5 | 0.5 | 3.20 | 4.61 | C1 = (1.5, 1) klynge1 | gruppe_1 |
| 4.30 | 3.54 | 0.71 | 0.71 | C2 = (4.5, 3.5) klynge2 | gruppe_2 |
A B C D
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 2 | 4 | 5 | X |
| 1 | 1 | 3 | 4 | Y |
Igjen, vi gjør klyngingsoppgavene basert på minimumsavstanden som vi gjorde før. Så etter å ha gjort det, fikk vi klyngematrisen som er den samme som G_1.
G_2 =
| EN | B | C | D | |
|---|---|---|---|---|
| 1 | 1 | 0 | 0 | gruppe_1 |
| 0 | 0 | 1 | 1 | gruppe_2 |
Som her, G_2 == G_1, så det kreves ingen ytterligere iterasjon, og vi kan stoppe her.
K-Means Implementering ved bruk av Python:
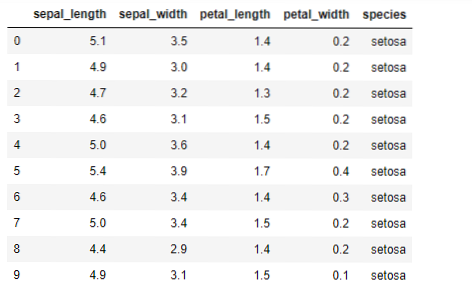
Nå skal vi implementere K-betyr-algoritmen i python. For å implementere K-middel skal vi bruke det berømte Iris-datasettet, som er åpen kildekode. Dette datasettet har tre forskjellige klasser. Dette datasettet har i utgangspunktet fire funksjoner: Sepal lengde, sepal bredde, kronblad lengde og kronblad bredde. Den siste kolonnen vil fortelle navnet på klassen på den raden som setosa.
Datasettet ser ut som nedenfor:
For implementeringen av python k-betyr, må vi importere de nødvendige bibliotekene. Så vi importerer Pandaer, Numpy, Matplotlib og også KMeans fra sklearn.clutser som gitt nedenfor:

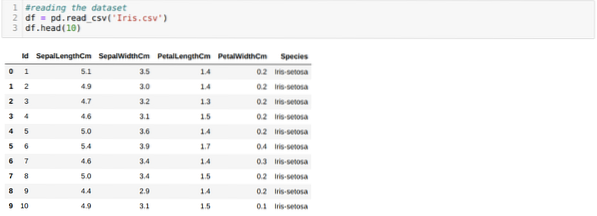
Vi leser Iris.csv datasett ved hjelp av read_csv pandas metode og vil vise de 10 beste resultatene ved hjelp av hodemetoden.
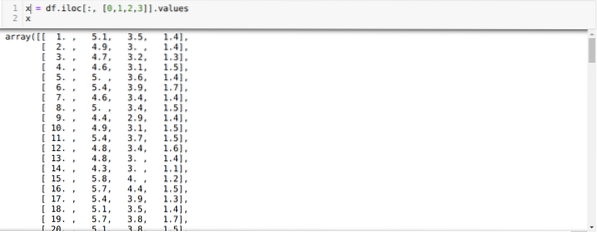
Nå leser vi bare de funksjonene i datasettet som vi krevde for å trene modellen. Så vi leser alle de fire funksjonene i datasettene (sepal lengde, sepal bredde, petal lengde, petal bredde). For det overførte vi de fire indeksverdiene [0, 1, 2, 3] til iloc-funksjonen til pandas dataramme (df) som vist nedenfor:
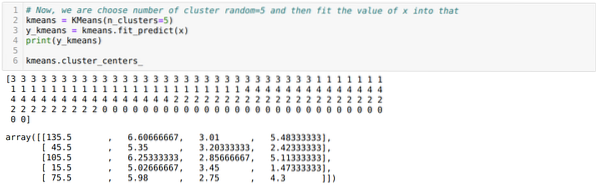
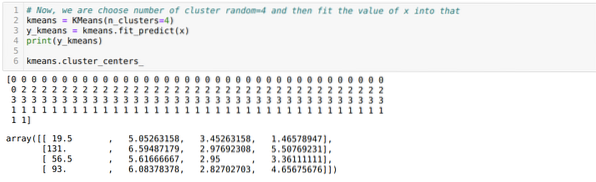
Nå velger vi antall klynger tilfeldig (K = 5). Vi oppretter objektet til K-middelklassen og passer deretter x-datasettet vårt til det for trening og prediksjon som vist nedenfor:
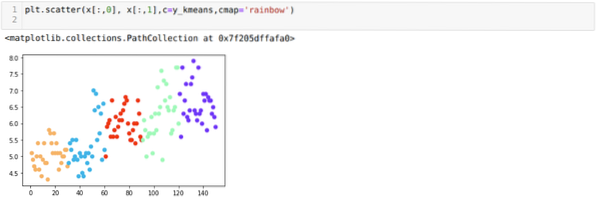
Nå skal vi visualisere modellen vår med den tilfeldige K = 5-verdien. Vi kan tydelig se fem klynger, men det ser ut til at den ikke er nøyaktig, som vist nedenfor.
Så vårt neste trinn er å finne ut om antallet klynger var nøyaktig eller ikke. Og for det bruker vi albuen-metoden. Elbow-metoden brukes til å finne ut det optimale antallet klyngen for et bestemt datasett. Denne metoden vil bli brukt for å finne ut om verdien av k = 5 var riktig eller ikke, ettersom vi ikke får klare klynger. Så etter det går vi til følgende graf, som viser at verdien av K = 5 ikke er riktig fordi den optimale verdien faller mellom 3 eller 4.
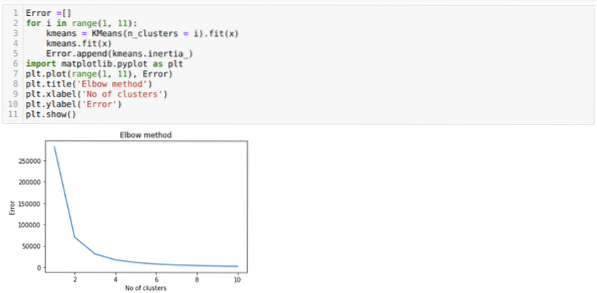
Nå skal vi kjøre ovennevnte kode igjen med antall klynger K = 4 som vist nedenfor:
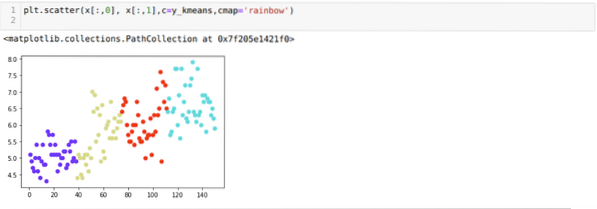
Nå skal vi visualisere ovennevnte K = 4 nybyggklynging. Skjermbildet nedenfor viser at nå er klyngingen gjort gjennom k-middel.
Konklusjon
Så vi studerte K-betyr-algoritmen i både numerisk og python-kode. Vi har også sett hvordan vi kan finne ut antall klynger for et bestemt datasett. Noen ganger kan ikke Albue-metoden gi riktig antall klynger, så i så fall er det flere metoder vi kan velge.
 Phenquestions
Phenquestions